Life and Injury

The Value of Life and Cost of Injury

Alongside attempting to value the environment providing a valuation for life is one of the most problematic quantification issues a researcher can face when performing a CBA. Valuing a human life is clearly controversial. Governments spend huge sums of money researching new treatments and developing drugs to improve the chance of a cancer patient surviving. However, in purely economic terms when considering a project a monetary value must be obtained for that life saved, so that the benefits of doing so can be quantified against the cost of new research and treatments. This is referred to as obtaining the value of statistical life.

Forgone Earnings or Constructive Method

This method of assigning a monetary value to life estimates what the individual would have earned if they had remained alive. The value of a life saved is therefore equal to that individual’s discounted future earnings. One key issue with this method of providing a monetary value for life is that it supposes that after retirement age an individuals life is worth zero, since there would be no loss of earnings should they die. This same problem is present with the valuation of full-time homemakers, or unpaid volunteers. There is also the potential issue dependent on the researcher and nature of the CBA being conducted that different individuals could be valued differently dependent on their wage rate. A CEOs life would be valued higher than a front line employee, as the CEOs forgone earnings are greater.

A second key problem exists with this method in that it does not account for the willingness to pay of individual for reduced risk of death, but instead measures lives based solely on forgone earnings. A more appropriate method may therefore be to collect data on the value individuals are willing to pay to reduce their risk of death.

Revealed Preference Method

Valuing life can be preformed using revealed preferences to estimate individual’s willingness to pay for reduced risk of death. Two main approaches exist relating to revealed preferences. These are:

(1) Consumer Purchase Studies

This method uses decision trees to estimate the value individuals place on the reduced risk of death through the purchase or non-purchase of safety devices, such as fire extinguishers, airbags in cars etc.

For example, the decision tree below can be used to provide a value for an individual’s life based on their decision to purchase a fire extinguisher for their home. The decision tree can be represented as follows:

VSL

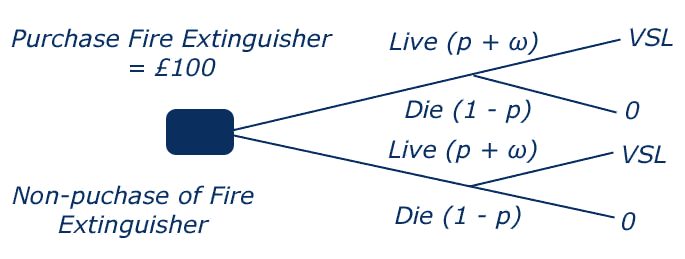
If an individual is assumed to be indifferent between the two options – purchase or non-purchase of the fire extinguisher – this can be represented as follows:

(p + ω) VSL- £a = PVSL

(p + ω) VSL - PVSL= £a

ωVSL = £a

VSL = £a/ω

Where £a is equal to the cost of the purchase of the safety device, and ω is equal to the reduction in risk associated with the purchase of this item. In our example of a fire extinguisher if the fire extinguisher costs £100 and the reduced risk of death is equal to 1/5,000 – that is if 5,000 individuals purchase fire extinguishers one statistical life will be saved – then we can substitute in these values to the equation as follows to provide an estimate for the value of this statistical life:

VSL = £500,000

(2) Labour Market Studies

This method estimates the value of reduced risk of death by looking at the additional compensation workers require in order to undertake riskier occupations. Using this method of measurement, the value of life can be calculated by gathering data on the compensation the worker requires in order to undertake the occupation with the greater risk of death (£a), and the change in fatality risk (or difference between the two occupations) which can be expressed as ω. The value of statistical life (VSL) can then be calculated using the following equation:

For example, suppose an RAF aircraft mechanic has a 1/500 greater chance of death than a commercial aircraft mechanic. The salary of the RAF mechanic is however higher pertaining to the greater risk involved in their occupation. They receive £5,000 more per year than the commercial aircraft mechanic. If workers are assumed to be indifferent between the two jobs, then we can estimate the value of life as follows:

VSL = £2,500,000

Life Insurance Valuations

Similar to the foregone earnings method this approach uses life insurance valuations as a measure of the cost of a lost life, or net benefit if a life is saved. For example, if a road improvement project is estimated to reduce fatalities on that stretch of road by 5 persons per year, then a value could be obtained for the net benefit by simply looking at average life insurance payouts for deaths on that stretch of road, or indeed using a national average.

Hedonic Method of Valuing Life

The hedonic method of valuing life as with other hedonic methods uses regression analyses to estimate the relative value of certain variables (Boardman et al, 2006, 352). It therefore can produce potentially better estimates of the value of life, as unlike consumer purchase and labour market methods, it does not necessarily omit variables that may have significant impacts on the relative valuation of certain safety devices or occupations.

For example, if a researcher is seeking to estimate the value of life through exploring labour market wage data, they may include variables on job tenure, education, age, and other factors which may impact on the relative wage offered in different occupations, as well as including data on injury and risk of death. The model could be expressed as follows:

This will offer the researcher a potentially more accurate estimate of the actual value of life associated with a certain occupation, as the relative impact of the other variables included in the model can be considered when calculating the hedonic price using the value of the β estimates.

Problems with valuing life

The key problem with developing quantifiable measures for life rest in the moral dilemma this creates. How can an insurance valuation provide an accurate value for the life of an individual? If the costs of saving that life are greater than this insurance valuation does this mean that a project should not go ahead? In purely economic terms this may be the case, and represents a significant concern in the quantification and use of CBA to appraise projects which aim to save lives.

Another problem faced by researchers is actually in estimating the number of lives that may be saved as an outcome of a given project. Regardless of which method of valuing life the researcher decides to use, the value for the number of lives saved could have a significant impact on the overall net benefits associated with a project and therefore the viability of a project.

Problems with Consumer Purchase and Labour Market Methods

A key problem which exists in the use of consumer purchase or labour market studies to estimate the value of statistical life regards information. Both methods assume that individuals will have full information concerning risks, for example the risk involved in performing a particular occupation. Some empirical studies have suggested that individuals over-estimate the likelihood of health risks or even death even though these events may actually have a very low probability. Similarly it is possible that individuals may under-estimate the probability of health risks or even death associated with certain occupations. This would lead to an incorrect low valuation of life. However, given a choice between performing a risky occupation where a chance of death exists compared to an occupation where almost no chance of death exists, the choice for many individuals will not be rational in economic terms i.e. based solely on probabilities, but instead many individuals will prove to be highly risk averse.

A second problem with these methods of valuing life lies in actually measuring risk associated with certain occupations. Limitations in data collection and levels of aggregation used when considering occupations may result in inaccurate estimations of the risks involved in some occupations. For example, consider a manufacturing firm. Wage data may be collected from this firm at the single factory level. However, this data would not accurately show the divisions in risk between a machine operator working in this factory who regularly interacts with highly toxic materials, and a manager who works in the office and has little interaction with the manufacturing ‘shop floor’. Using factory level aggregated data would result in estimates of the probability of injury or death being too low for the shop floor machine operator, but too high for the manager.

The third problem with these methods of valuing statistical life is that most individuals will experience a diminishing marginal utility from increases in safety. For example, the purchase of a car with seat belts will have a significant impact on the individual providing them with a substantial increased utility from the increase in safety they associate with this safety device. A car which has seat belts and also an air bag has a further but decreasing impact on the individual. Meanwhile, a car with seat belts, air bags, and assisted breaking provides only a small marginal increase in utility. This affects the willingness to pay an individual feels towards these safety devices. Most individuals would be willing to pay a significant amount for the first safety device, but then diminishing amounts for further safety devices they view as only having minor impacts in improving the overall relative safety of the car.

Finally, these methods again suffer in some of the assumptions used in their measures. These methods assume markets are efficient, that is, that wages are representative of the risk involved in occupations. In reality a number of factors influence occupation wage structures, including trade union bargaining, different job characteristics, skill levels, educational requirements associated with occupations, and other external factors.